心理ネットワーク入門1:横断データ
心理ネットワークとは?
心理ネットワーク(精神病理ネットワーク)については,まずは以下の2つの論文を読んでください。以降は,それを前提として,技術的な側面のみを解説します。
- 樫原 潤・伊藤正哉(印刷中) 心理ネットワークアプローチがもたらす「臨床革命」—認知行動療法の文脈に基づく展望— 認知行動療法研究
- 樫原 潤(2019) 精神病理ネットワークの応用可能性―うつ病治療のテイラー化を促進するために― 心理学評論 62(2),143-165
心理ネットワークとは,観察可能な変数を表すノードと統計的関係を表すエッジから構成されるものです(Epskamp, Borsboom & Fried, 2018 以下の内容は基本的にEpskamp et al., 2018に従っています)。心理ネットワークモデルは,因子分析やSEMなどのように潜在変数を仮定してそれから各項目・症状を説明するのではなく,症状(心理変数)間のネットワーク構造を検討します。
心理ネットワークは,以下の図のように,観察可能な変数を表すノードは円で,関係を表すエッジは線でプロットされます。
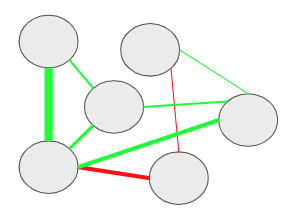
心理ネットワーク分析の手順
心理ネットワーク分析は,おおよそ以下の4ステップからなります。
- 統計的手法によってノード間のエッジを推定する
- 推定された統計的関係をもとにネットワークを図示する
- ネットワーク特性の指標の検討する
- ネットワークの精度の検討する
ここで注意すべき点は,一般的なネットワーク科学で扱うネットワークの場合は,エッジは観察可能です(例えば,電力網ネットワークのエッジは直接観察・測定可能です)。しかし,心理ネットワークのエッジは,データから推定されます(重み付けネットワーク)。そのため,サンプルサイズの影響も受けますので,ネットワークのエッジの精度も検討する必要があります。また,ネットワーク科学では,グローバルなネットワーク特性の指標が使われます(small worldness, density, global clustering)。しかし,心理ネットワークのような重み付けネットワークでは使えません。そのため,2つのノードの関係や1つのノードがどのような影響力をもつのか(中心性の指標)といったローカルなネットワーク特性を用いることが多いです。
有向・無向ネットワーク
心理ネットワークの話の前に,有向ネットワークと無向ネットワークについて説明をしておきます。まず,有向ネットワークとはエッジに方向性があるネットワークになります。以下の図ようにエッジが矢印になっているネットワークです。この矢印の方向には因果関係が想定されています。例えば,「活動性低下→抑うつ気分増加」となっていましたら,活動低下が原因で抑うつ気分増加するという意味になります。ただし,「活動性低下→抑うつ気分増加」と聞いて,「活動性低下←抑うつ気分増加」もありえるのではないかと感じた方もおられるかもしれません。そのとおりでして,因果関係を言うには,まず原因は結果に時間的に先行する必要がありますし,因果に関連する変数が全て測定された上で,原因と結果が巡回しない(非巡回)必要があります。観察研究によって収集された心理学のデータの場合,時間的な前後関係は時系列データによって示せても,非巡回となるとかなり難しいかと思います。そのため,横断データに対する心理ネットワークでは,エッジに方向性がない無向ネットワークが用いられます。
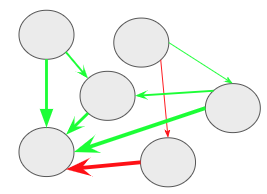
2つのノードの関係(エッジの符号)
横断データに対する心理ネットワークでは,エッジに方向性がない無向ネットワークが用いられます。エッジの色は符号を意味していて,青もしくは緑の場合は正,赤の場合は負を表します。エッジが正(青色もしくは緑色)の場合は,2つのノード間には正の関係性が存在します(片方が増えると,もう一方も増える)。エッジが負(赤色)の場合は,2つのノード間には負の関係性が存在します(片方が増えると,もう一方は減る)。また,エッジの太さは,関係の強さを意味します。この場合の関係の強さとは,全体のノードからの影響を考慮した時の2つのノード間の関係の強さになります。そして,エッジの長さは,エッジの強さの逆数になります。つまり,ノード間の関係が強ければ強いほど,エッジの長さが短くなります。分かりやすいか微妙な例ですが,パーティ会場で関係性の近い2人のコミュニケーションは近い距離でなされるイメージをもつと良いかなと思います。

ノードの中心性指標
心理ネットワークは,重み付けネットワークのため,その他のネットワークと違って,グローバルなネットワーク特性の指標(small worldness, density, global clustering)が使えません。そこで,各ノードの他のノードの影響性のようなローカルなネットワーク特性(中心性指標)を用います。そのようなローカルなネットワーク特性としては,strength,closeness,betweenessの3つがあります。
Strength
Strength(重み付けのないネットワークの場合は,degreeと言う)は,あるノードがつながっている全てのエッジの強さを合計したものです。あるノードが他のノードとどのくらい強くつながっているのかを表す指標であり,そのノードの全体に対する影響力を表しているといえます。
以下のようなネットワークを例にして,ノード1のStrengthを計算してみましょう。ノード1とノード2の間には,0.3の緑のエッジがあります。ノード1とノード3の間には,0.1の緑のエッジがあります。ノード1とノード6の間には,0.2の緑のエッジがあります。最後にノード1とノード4の間には,0.2の赤のエッジがあります。これらを合計した0.8がノード1のStrengthになります。ここの計算では,エッジの正負は問われません。なお,Strengthは接続しているノードの合計ですので,ノードが増えるほど大きくなるのでプロットする際には標準化されます。これは他の指標も同様です。
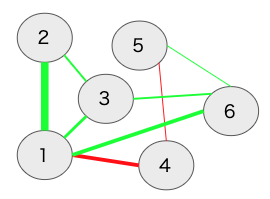
Closeness
Closenessは,あるノードと他の全てのノード間の最短経路長の合計の逆数になります。なにそれ?と思ったかもしれません。まず,ノード間の最短経路長とは,あるノードから別のノードまで最短距離でいける距離です。この距離というのは,エッジの強さの逆数になります。つまり,エッジの強さが0.1ならばその逆数は1/0.1で10になり,エッジの強さが0.5ならば1/0.5で2になります。最短経路長は,この距離を使って,あるノードから別のノードまでの距離を計算して,最も短い距離でいける距離を計算します。そして,あるノードへの他の全てのノードとの最短経路長を計算して,合計したものの逆数がClosenessになります。
ちょっと具体例で計算してみましょう。以下の図で,ノード1からノード3の最短経路長を調べてみましょう。ノード3からノード1に行くには,(1)ノード3からノード1に直接移動する,(2)ノード3からノード2を経由してノード1へ移動する,(3)ノード3からノード6を経由してノード1にいくの3つがあります。まず,(1)のノード1から3への直接経路については,ノード1と3のエッジの強さは0.1なので距離は10です。次に,(2)のノード2を経由する間接経路は,ノード3と2のエッジが0.1で距離10,ノード2とノード1のエッジが0.3で距離3.33なので,合計13.33になります。最後に,(3)のノード6を経由する間接経路は,ノード3と6のエッジが0.05で距離20,ノード6とノード1が0.2で距離5なので合計25となります。(1)(2)(3)を比較すると,ノード1から3の直接経路の長さが最短経路長となります。ただ,もしノード3と2のエッジが0.2の場合は,ノード2を経由する間接経路が最短経路になります。なお,以下の図は,手作業で作ったので強さと距離んの関係が適切ではありません,ご理解のほどよろしくお願いいたします。
このような感じで,あるノードから他のノードまでの最短経路長をそれぞれ計算していって,それらを合計したものの逆数がClosenessになります。Closenessは,あるノードがどのくらい間接的な影響を含めて他のノードとつながっているのかを示しています(一方,Strengthは,あるノードがどのくらい直説的に他のノードとつながっているのかを示しています)。つまり,あるノードから他のノードへの拡散の速さを表現していると言えます。

Betweeness
Betweennessは,2つのノード間の最短経路上に,あるノードが何回あるのかを示しています。先程,Clonenessで最短経路を計算しましたが,その最短経路上に,特定のノードが登場する回数を見ることで,そのノードが影響性の流れにおいてどの程度の影響力を持つのかを検討できます。以下の図の場合,ノード4と2の最短経路は,ノード4からノード1を経由してノード1に行くというものです。このように,ノード4とノード2の最短経路上には,ノード1があります。このようにして,特定のノード(今回はノード1)が最短経路上に何回出てくるのかカウントすることでBetweenessが計算できます。このように,Betweennessは,あるノードが2つのノードの接続においてどのくらい重要かを示すものです。このノードによっては,影響性の流れを変えることができるので,心理的介入などにおいても重視される指標といえるかもしれません。

Gaussian Graphical Model(GGM)
変数間の関係がある・ないというグラフを作る場合に,確率分布と結びつけるようなモデルのことをベアワイズ・マルコフ・グラフ(pairwise Markov graph)と呼びます。そして,心理ネットワークで用いる無向ネットワークモデルの推定では,ペアワイズ・マルコフ確率場(pairwise Markov random field)がよく使われます。さらに,無向ネットワークでも,データが連続かつ正規分布の場合には,多変量正規分布を用いたGaussian Graphical Model(GGM)が用いられます。心理学で収集するデータは,連続変数かつ正規分布を仮定できることも多いので,心理ネットワーク分析ではGGMがよく用いられます。
GGMでは,以下のように,\(y_{C}\) は平均0, 分散共分散行列 \(\mathbf{\Sigma}\) の多変量正規分布に従う。ここでのyは確率変数ベクトルYの実現値で,中心化をしたものである(中心化は値から平均値を引く手続きです)。\(y_{C}\) のCはcaseつまりデータフレームの行に対応しており,yはベクトルなので,1つの値ではなく複数の変数が収められている(例. y[c=1,1]は1人目の不安得点,y[c=2,1]は2人目の不安得点, y[c=1,2]は1人目のうつ得点など)。そして,分散共分散行列 \(\mathbf{\Sigma}\)は,ベクトルyに含まれる変数間の分散共分散行列になります。
\[ y_{C} \sim N(\mathbf{0}, \mathbf{\Sigma}) \]
分散共分散行列→精度行列→偏相関行列
GGMでは,\(y_{C}\) は平均0, 分散共分散行列 \(\mathbf{\Sigma}\) の多変量正規分布に従うとして,その分散共分散行列から偏相関行列を算出します。具体的な手続きとしては,分散共分散行列からその逆行列である精度行列を計算し,精度行列から偏相関行列を計算します。なんだかややこしそうですが,そうでもありません。
まず,Kは精度行列です。この精度行列Kは,分散共分散行列の逆行列になります。
\[ \boldsymbol{K}=\boldsymbol{\Sigma}^{-1} \]
逆行列って何?ってなるかもしれないのですが,逆行列は,n次正方行列Aに掛けた場合に以下のような単位行列Eとなるような行列のことです。分散共分散行列に何か行列をかけ合わせた時に,以下のような単位行列Eになるようなものがここで知りたい逆行列です。どうやって逆行列計算するの?って思われたかもしれませんが,以降はパソコンに頼ってRで計算させつつ分散共分散行列から精度行列を経由して,偏相関行列を計算してみましょう。
\[\boldsymbol{E}=\left[\begin{array}{lcc}1 & 0 \\ 0 & 1\end{array}\right]\] 以降の計算は,Epskamp, Waldorp, Mõttus & Borsboom(2018)に記載されている例を用います。まず,以下のような分散共分散行列( \(\mathbf{\Sigma}\) ) Aを使って,これを偏相関行列にします。Aは以下の通りです。Rで計算できますので,以下をコピペして実行ください。変数1と変数2は負の関連があり,変数1と変数3は正の関連があり,変数2と変数3は関連は弱そうです。
A <- matrix(c(1,-0.26,0.31,-0.26,1,-0.08,0.31,-0.08,1), 3, 3)
A## [,1] [,2] [,3]
## [1,] 1.00 -0.26 0.31
## [2,] -0.26 1.00 -0.08
## [3,] 0.31 -0.08 1.00さて,この分散共分散行列Aの逆行列,つまりAの精度行列を計算しましょう。手計算だと大変なので,ここはサクッとRのsolve()関数に計算させます。以下を実行ください。精度行列では,一部符号が逆転していますね(必ずではないです)。逆行列の計算では,特定の変数間の関連について他の変数の影響も考慮することになります。そのため,この精度行列(分散共分散行列の逆行列)を使って,偏相関行列を求めることができます。なお,逆行列が存在する行列は正則行列と呼ばれます。
inv_A <- solve(A)
inv_A## [,1] [,2] [,3]
## [1,] 1.1789330 0.2790710919 -0.3431435365
## [2,] 0.2790711 1.0725015306 -0.0007119161
## [3,] -0.3431435 -0.0007119161 1.1063175430以下の式を使って,上記で算出した精度行列から偏相関係数を求めることができます。
\[\operatorname{Cor}\left(Y_{i}, Y_{j} \mid \boldsymbol{y}_{-(i, j)}\right)=-\frac{\kappa_{i j}}{\sqrt{\kappa_{i i}} \sqrt{\kappa_{j j}}}\] これは手計算でも簡単にできるのですが,現代人なので,Rのstatsパッケージのcov2cor関数を使って偏相関行列を計算をしちゃいましょう。あまり大きな変化はないかもしれませんが,変数2と3の関係が分散共分散行列行列よりも小さくなり,関係がないと言ってもよいかと思われます。この偏相関行列の偏相関係数をエッジにしてネットワークを描きます。
library(stats)
-1 * cov2cor(inv_A)## [,1] [,2] [,3]
## [1,] -1.0000000 -0.2481826016 0.3004632529
## [2,] -0.2481826 -1.0000000000 0.0006535667
## [3,] 0.3004633 0.0006535667 -1.0000000000GGMは比較的シンプルなもので,多変量正規分布の分散共分散行列から偏相関行列を計算して,それを用いてネットワークを書くというものです。
クロスセクショナルデータのGGM
GGMは上記で説明をしたように,推定は簡単なので,最尤推定,最小二乗法,ベイズどれを使っても良いです。ただし,精度行列を求める方法としては,分散共分散行列の逆行列の計算でもできるけど,ネットワークのエッジが多すぎるとネットワークの理解がしにくくなります。そのため,ネットワークを疎(sparse)にするような手法が用いられることが多いです。そのような手法の1つとして,正則化(regularization)があります。正則化は,機械学習などにおいて発展してきた手法で,モデルの複雑さに罰則をかけて,過学習を避けるような手法です。ざっくり説明すると,多数の変数を使って予測をする場合に,影響力が弱い変数の影響をゼロに近づけるような工夫を導入することで,不要なエッジを除くことができる。影響力は弱いけそ存在している変数が減るとモデルが複雑じゃなくなりますが,複雑さに罰則をかけると,影響力は弱いけそ存在している変数の影響をゼロに近づけるようになります。このようにして,解釈に置いて煩雑なエッジを減らすことができます。GGMでは,LASSO(least absokute shrinkage and selection operator)が使われます。特にLASSOの一種のGraphical LASSOは,精度行列に直接的に罰則をかけられ,分散共分散行列があれば計算でき,一般的に他の方法よりも早いです。そして,このGLASSOのパラメータ調整では,EBICを使うのが推奨されています。
GGMの解釈法
GGMで計算されるエッジはどのように解釈されるでしょうか?まず,偏相関になりますので,通常の2変数間の相関係数ではなく,2変数以外の影響も考慮した2変数の関係になります。なので,ネットワークに含まれる変数の違いによっては,値が異なる可能性もありますし,2変数だけでなくネットワーク全体を考慮した解釈が必要になります。その際の解釈としては,つい「変数Aによって変数Bが引き起こされた」のような因果に踏み込んだ解釈をしてしまいますが,横断データのGGMで得られたエッジからそのような方向性をもった解釈は難しいです。できる解釈としては,(1)予測可能性の示唆と(2)因果関係の示唆になります。まず,因果関係は不明ではありますが,他の変数の影響を考慮しても,ある変数から別の変数が予測できているとはいえるので,A-B-Cという形でエッジがある場合に,BはAかCを予測する可能性があります。もちろん,最終的には縦断調査によって予測ができるかどうか検証する必要はあります。次に,因果関係の仮定を満たすことはできないし,効果の方向性は不明だが,そのエッジにはなんらかの因果的な効果がある可能性はあります。この結果を踏まえて,より因果関係に踏み込めるような研究を行うことができると思います。どちらも歯に物が挟まったような表現ですが,多くの場合心理ネットワークは探索的に実施されることからも,強い理論的予測による仮説検証の結果のような解釈をしないように気をつける必要があります。
ネットワークの正確度(accurary)
エッジは統計的に推定されるものなのでサンプルサイズの影響をうけます。ノードが増えると推定するパラメータはどんどん増えるので一般的な心理学研究では,サンプルサイズが足りないこともあります。そのため,ネットワークの正確度についても検討しておく必要があります(ネットワークの正確度については,Epskamp, Borsboom,& Fried (2018)に詳しいです)。
エッジの重みと中心性指標の精度の検証方法は,以下の3ステップになります(Epskamp, Borsboom,& Fried, 2018)。
- ブートストラップされた信頼区間をプロットすることでエッジの重みの正確度を検討する。
- データのサブセットを用いた場合の中心性指標の安定性(Stability)を検討する。
- エッジの重みと中心性指標間でブートストラップ差異検定行って,それらが有意に異なるのかを検討する。
心理ネットワーク分析を用いた際には1は必ず実施しますが,2と3については中心性に関心があるか差異検定に関心があるかによって実施を検討します。詳しくは,以降のRでの心理ネットワーク分析で触れます。
Rパッケージ
偏相関行列の計算自体は複数のRパッケージで可能になりますので,心理ネットワーク分析に使えるRパッケージは複数あります。ただし,心理ネットワーク分析の中心地でもあるアムステルダム大学のSacha Epskampが開発したqgraphとbootnetがあれば,横断データの心理ネットワーク分析は実施できます。なお,あとで説明するブリッジ中心性指標はnetworktools,ネットワークの比較はNetworkComparisonTestを使用します。
- qgraph:ネットワークのプロットと推定
- bootnet: 様々な種類のネットワーク推定,ネットワークの正確度の検討
- networktools:ブリッジ中心性を含むノードの検討に有用なツール
- NetworkComparisonTest: ネットワークの比較検定
なお,アムステルダム大学で開発しているベイズ統計と頻度論統計のGUIソフトウェアであるJASPには,心理ネットワーク分析が組み込まれており,簡単に実施して見る上ではかなり有用と思います。JASPは国里を含む日本語化チームにより2021年9月(v0.15)より一部が日本語化されています。心理ネットワーク分析の説明は,こちらをご確認ください。
心理ネットワーク分析を試してみよう!
さて,以下では,実際にRで心理ネットワーク分析を実行してみましょう。その題材として, Jordan, P., Shedden-Mora, M. C., & Löwe, B. (2017). Psychometric analysis of the Generalized Anxiety Disorder scale (GAD-7) in primary care using modern item response theory. PloS One, 12(8), e0182162.を選びました。この研究は,不安の症状評価で用いられるGAD-7について項目反応理論を用いた検討を行った研究です。Hamburgのプライマリケアを受診した3404名からGAD-7(全般性不安),PHQ-9(うつ),PHQ-15(身体症状)データを収集しており,比較的サンプルサイズが大きいのと,雑誌のサイト上でデータを公開していることから,以下の心理ネットワーク分析の練習で使ってみましょう。
使用するRパッケージの読み込み
Jordan et al.(2017)のデータがSPSS形式で配布されているのでSPSS形式のデータを読み込むforeignパッケージとデータ処理用にtidyverseパッケージを読み込みます。そして,心理ネットワーク分析では,上述したbootnetパッケージとqgraphパッケージを読み込みます。
library(tidyverse)
library(foreign)
library(bootnet)
library(qgraph)データの読み込み
Jordan et al.(2017)のデータを雑誌のサイトからdownload.fileでダウンロードして,それを読み込みます。変数名がややこしかったので,renameで名前を変更しています。
download.file("https://doi.org/10.1371/journal.pone.0182162.s004","pone.0182162.s004.sav")
data <- read.spss("pone.0182162.s004.sav",
to.data.frame=TRUE)
# データの整理
data_gad <- data %>%
rename(gad7a = S_GAD7_a, gad7b = S_GAD7_b,
gad7c = S_GAD7_c, gad7d = S_GAD7_d,
gad7e = S_GAD7_e, gad7f = S_GAD7_f,
gad7g = S_GAD7_g, phq9a = S_PHQ9_a,
phq9b = S_PHQ9_b, phq9c = S_PHQ9_c,
phq9d = S_PHQ9_d, phq9e = S_PHQ9_e,
phq9f = S_PHQ9_f, phq9g = S_PHQ9_g,
phq9h = S_PHQ9_h, phq9i = S_PHQ9_i) %>%
select(gad7a, gad7b, gad7c, gad7d, gad7e, gad7f, gad7g)ネットワークの推定とプロット
早速,エッジの推定をしましょう。bootnetパッケージのestimateNetwork()関数を使います。エッジの推定にあたり,EBICでモデル選択して,パラメータ調整をするGLASSOを使います(defaultで”EBICglasso”を指定する)。GAD-7は,不安症状について,「まったくない」から「ほとんど毎日」の4件法で頻度を問います。これは,順序変数と考えられるので,通常の分散共分散ではなくて,ポリコリック相関(順序変数の相関)を計算します。corMethodで “cor_auto”を指定すれば,自動的に順序変数にはポリコリック相関を計算してエッジの推定をしてくれます(なお,“cor_auto”では7件法以下は順序変数として扱います)。
results_gad <- estimateNetwork(data_gad,default = "EBICglasso", corMethod = "cor_auto")推定したエッジをネットワークとしてプロットしてみましょう(layoutは”spring”を指定します)
plot(results_gad, layout = "spring",labels = TRUE)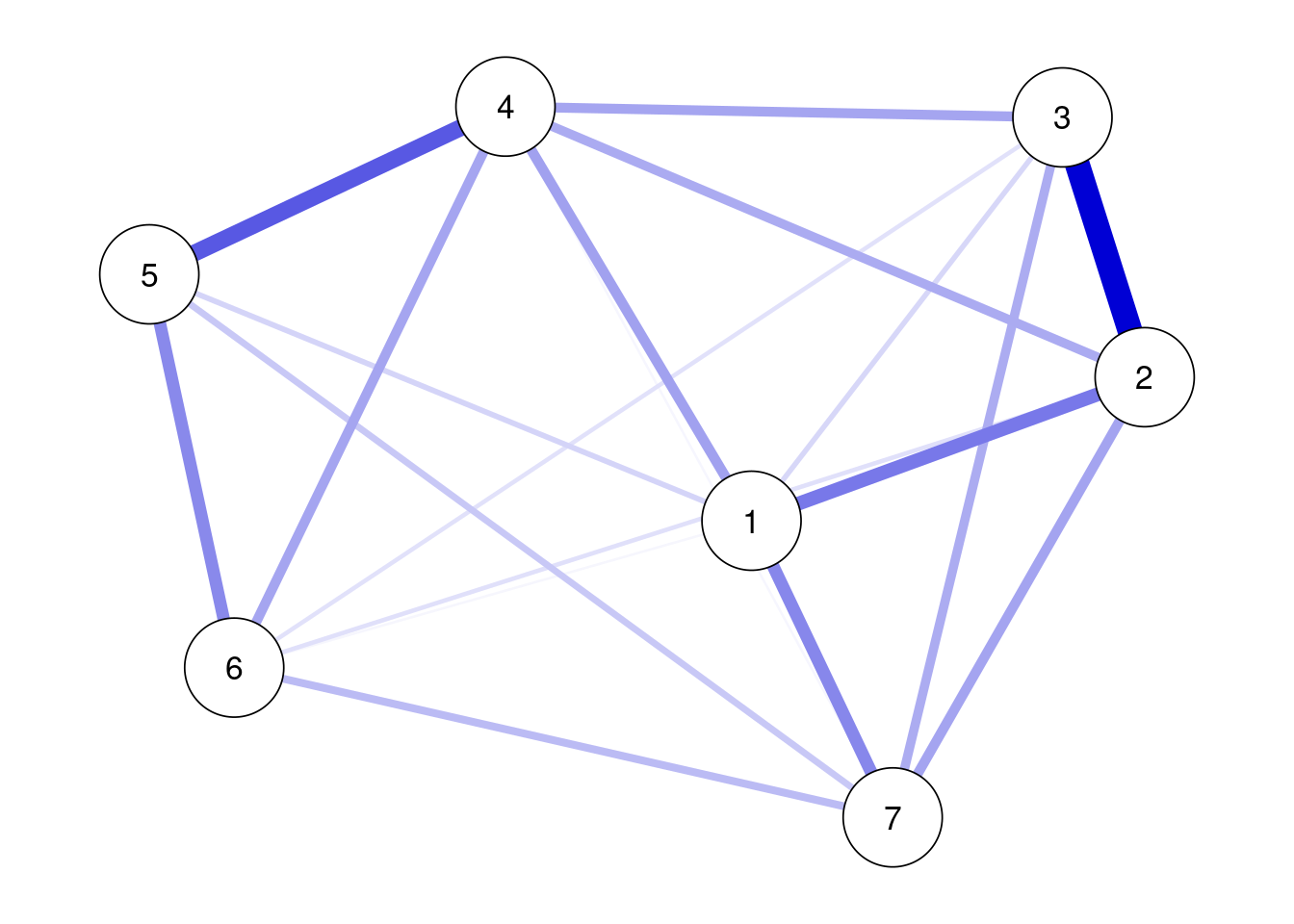
エッジの重みの正確度
エッジの重みの正確度を評価する方法として,95%信頼区間を使う方法があります。その際に,ブートストラップ法を用いる。ブートストラップ法は,データ元から復元抽出(無作為に取り出したデータを戻してから取り出すことを繰り返すこと,つまり同じデータを取り出すことがある)を繰り返して,何度も取り出したデータから推定値を計算して,誤差などの性質を明らかにする方法です。95%信頼区間もブートストラップ法を用いて計算できます。
ブートストラップ法には,ノンパラメトリックとパラメトリックがあります。ノンパラメトリックブートストラップは常に使えますが,パラメトリックブートストラップはデータのパラメトリックモデルがある場合のみ使用できます。基本的にはノンパラメトリックブートストラップを使います。正則化されてない,ノンパラメトリックでは結果が不安定である,ノンパラとパラメトリックで比較したい場合のみパラメトリックブートストラップを使います。
ちなみに,ブートストラップで推定した95%信頼区間は,0をまたぐかどうかで有意性の確認にも使えますが,心理ネットワークモデルの場合は正則化されているので,避けるほうが良い。あくまで,エッジの重みの正確度を調べるために使いましょう。
それでは,エッジの重みの正確度を推定をしましょう。bootnetパッケージのbootnet()関数を使います。先程推定した結果を使って,nBootsでサンプル数を決めます。プロットをなめらかにするために2500サンプルにします。nCoresで並列処理をして計算を高速化します。以下では,4コアにしていますが,お手持ちのPCのコア数に合わせて変更ください。なお,国里のゼミ生でサーバーを使っている人は,コアは1つで実行してください。コア4つ以上ある方は,コメントアウトした方を利用ください)中心性指標も計算するために,statisticsで指定をします。
accuracy_edge <- bootnet(results_gad, nBoots = 2500, nCores =4, statistics = c("edge", "strength", "closeness", "betweenness"))summaryで推定結果を確認できます。ただ,以下のプロットのほうが確認がしやすいです。
summary(accuracy_edge)## # A tibble: 42 × 17
## type id node1 node2 sample mean sd CIlower CIupper q2.5 q97.5
## <chr> <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 betw… gad7a gad7a "" 2 1.54 1.19 -0.377 4.38 0 4
## 2 betw… gad7b gad7b "" 2 3.11 1.87 -1.73 5.73 2 8
## 3 betw… gad7c gad7c "" 0 1.70 2.41 -4.81 4.81 0 8
## 4 betw… gad7d gad7d "" 12 9.37 2.27 7.47 16.5 4 12
## 5 betw… gad7e gad7e "" 0 1.10 2.01 -4.01 4.01 0 8
## 6 betw… gad7f gad7f "" 0 0.374 0.800 -1.60 1.60 0 2
## 7 betw… gad7g gad7g "" 0 1.18 1.68 -3.35 3.35 0 6
## 8 clos… gad7a gad7a "" 0.0257 0.0257 0.00148 0.0227 0.0286 0.0227 0.0284
## 9 clos… gad7b gad7b "" 0.0260 0.0264 0.00155 0.0229 0.0291 0.0237 0.0296
## 10 clos… gad7c gad7c "" 0.0252 0.0257 0.00171 0.0217 0.0286 0.0226 0.0290
## # … with 32 more rows, and 6 more variables: q2.5_non0 <dbl>, mean_non0 <dbl>,
## # q97.5_non0 <dbl>, var_non0 <dbl>, sd_non0 <dbl>, prop0 <dbl>それでは,プロットしてみましょう。サンプルサイズが大きいためか,95%信頼区間の幅が狭いですね。
plot(accuracy_edge, labels = FALSE, order = "sample")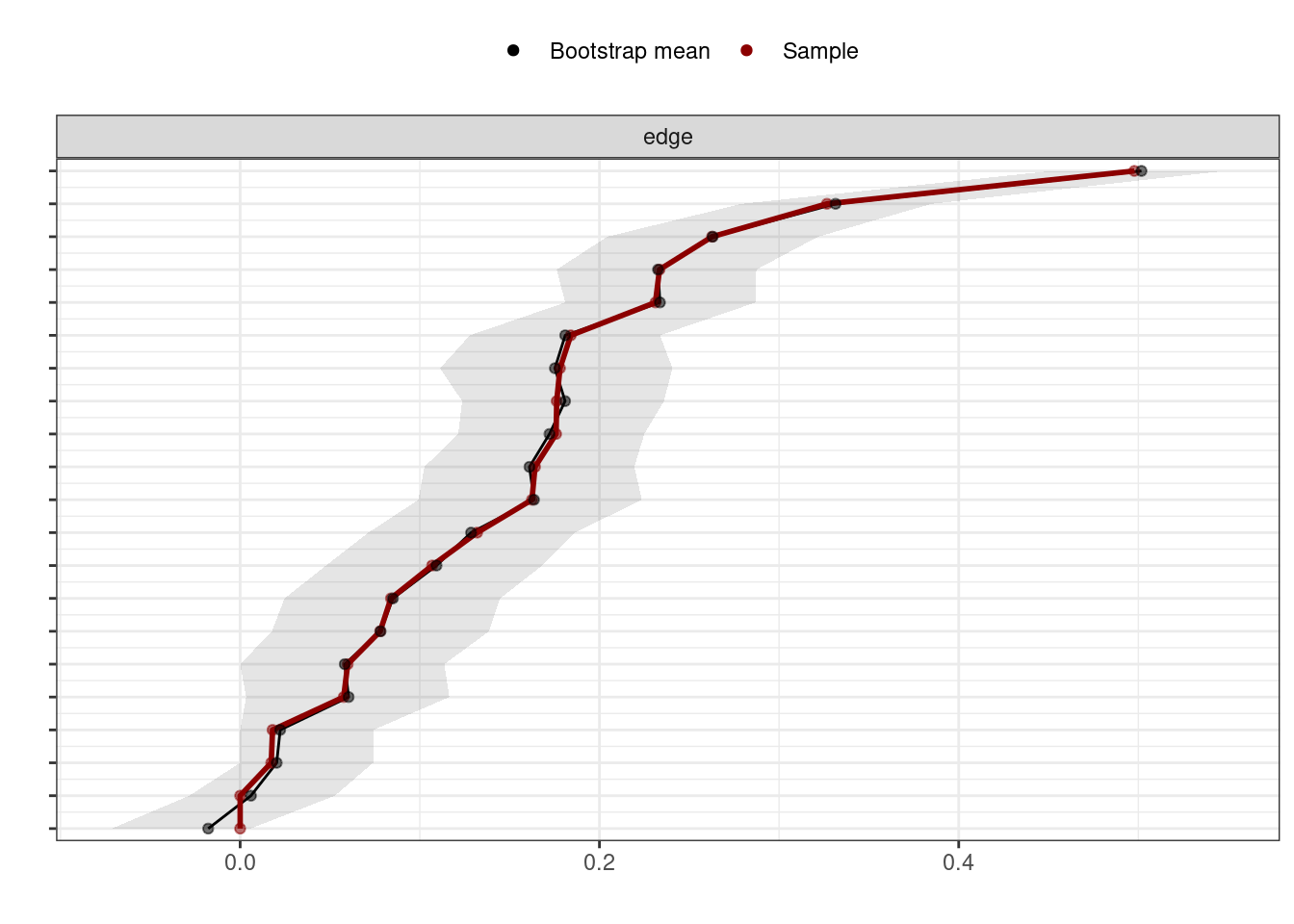
中心性の指標のプロット
中心性の指標は,qgraphパッケージのcontralityPlot関数でプロットできます。中心性指標は複数あるので,includeで”Strength”, “Betweenness”, “Closeness”の3つを指定します。
centralityPlot(results_gad, include = c("Strength", "Betweenness", "Closeness"))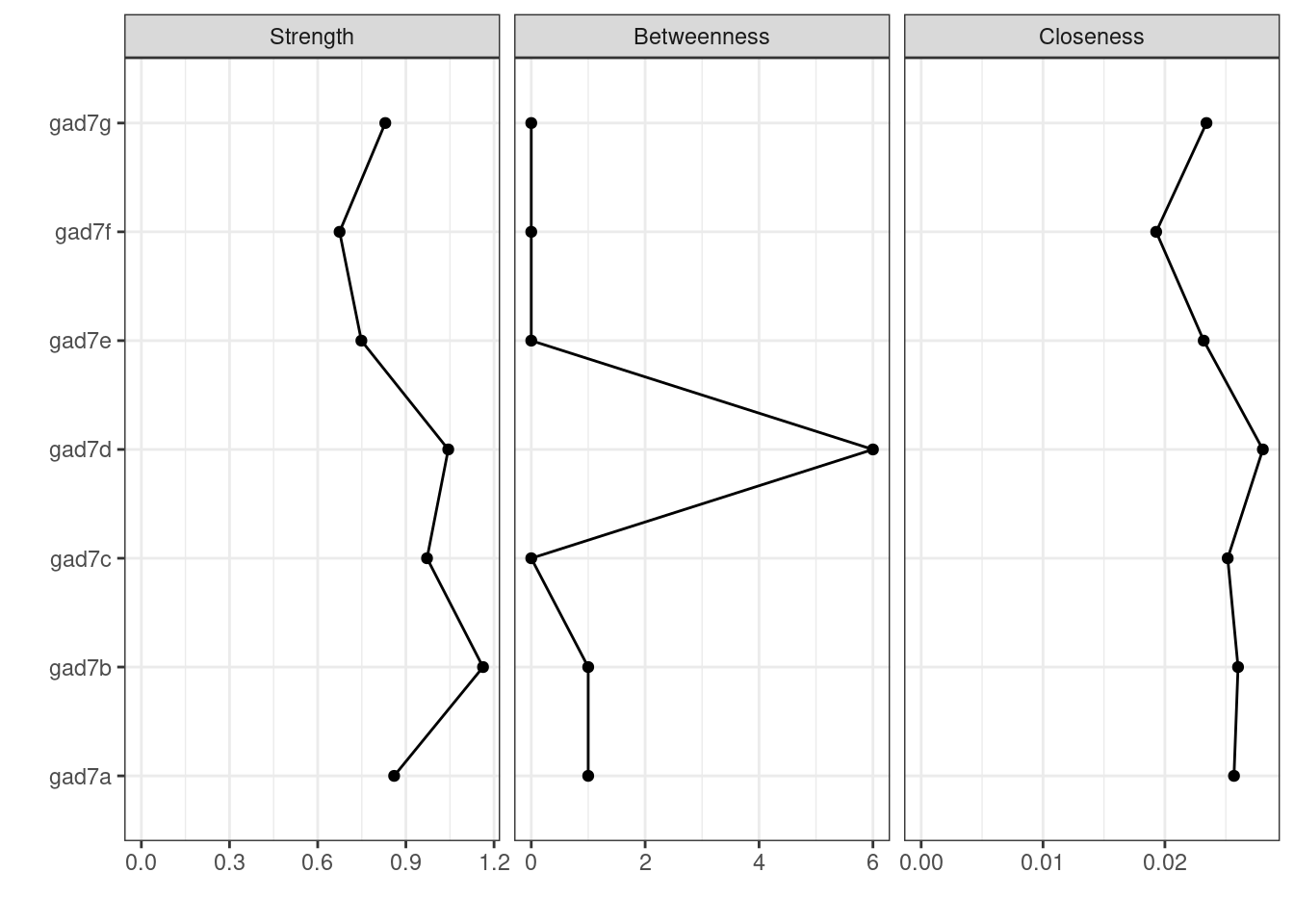
中心性指標の安定性(Stability)
中心性指標の正確度の解釈ができるように,データのサブセットを用いて,中心性指標の順序がどのくらい安定しているか検討します。具体的には,参加者を減らしていった場合(ケースドロップ)もしくはノードを減らしていった場合(ノードドロップ)にどのくらい中心性指標の順序が安定しているかを検討します。ノードドロップは解釈が難しくなるので(ノードをへらすと別のネットワークになるのは当然なので評価しにくい),ケースドロップを使用するのが良いかと思います。
中心性指標の安定性は,CS係数(correlation stability coefficient)によって評価します。CSはドロップできるケースの最大比率を表現しています。具体的には,参加者数を減らしていった場合に,元の中心性指標とドロップした中心性指標間に0.7以上の相関がブートストラップしたサンプルの95%にあるような最大のドロップケース比率である。多少恣意的な基準にはなるが,中心性の解釈をする上では,CS係数が0.25未満は不適切であり,できればCS係数は0.5を越えている必要がある(Epskamp, Borsboom, & Fried, 2018)。
中心性指標の安定性は,エッジの重みの正確度と同様にbootnetを使います。typeで”case”を指定するとケースドロップ時の安定性を推定します。なお,中心性の指標は複数あるので,statisticsで”strength”, “closeness”, “betweenness”を指定します。なお,国里のゼミ生でサーバーを使っている人は,コアは1つで実行してください。
stability_centrality <- bootnet(results_gad, nBoots = 2500, type = "case", nCores =4, statistics = c("strength", "closeness", "betweenness"))プロットして確認します。
plot(stability_centrality, c("strength", "closeness", "betweenness"))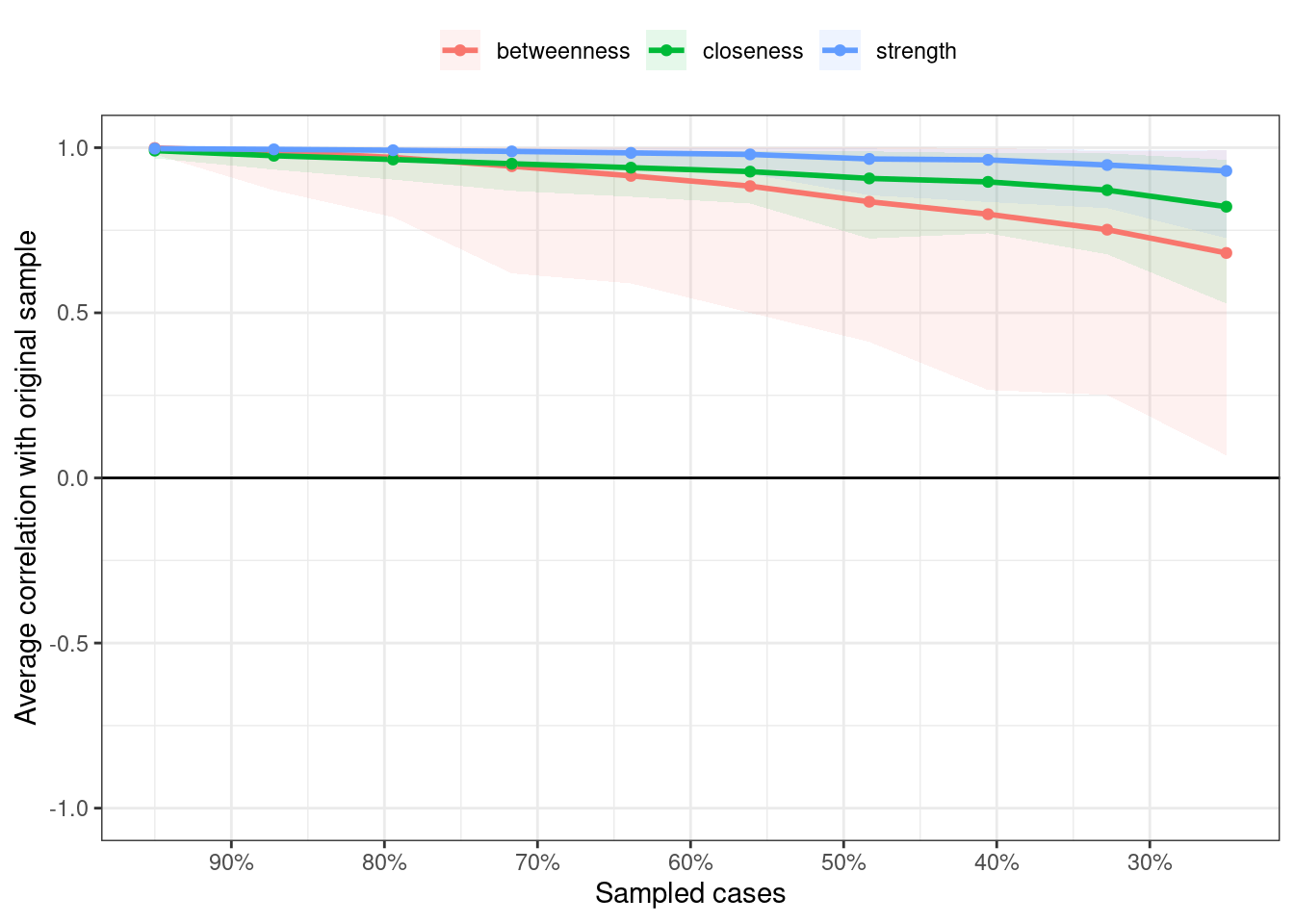
CS係数を確認します。StrengthとClosenessはCS係数が0.5を超えていますが,Betweenessの順序については,解釈ができません。
corStability(stability_centrality)## === Correlation Stability Analysis ===
##
## Sampling levels tested:
## nPerson Drop% n
## 1 851 75.0 231
## 2 1116 67.2 261
## 3 1381 59.4 209
## 4 1645 51.7 236
## 5 1910 43.9 259
## 6 2175 36.1 277
## 7 2440 28.3 254
## 8 2704 20.6 279
## 9 2969 12.8 254
## 10 3234 5.0 240
##
## Maximum drop proportions to retain correlation of 0.7 in at least 95% of the samples:
##
## betweenness: 0.283
## - For more accuracy, run bootnet(..., caseMin = 0.206, caseMax = 0.361)
##
## closeness: 0.672
## - For more accuracy, run bootnet(..., caseMin = 0.594, caseMax = 0.75)
##
## strength: 0.75 (CS-coefficient is highest level tested)
## - For more accuracy, run bootnet(..., caseMin = 0.672, caseMax = 1)
##
## Accuracy can also be increased by increasing both 'nBoots' and 'caseN'.有意差検定
ブートストラップを活用して,エッジの重みの比較や中心性指標の比較もできる。例えば,項目1と項目2のエッジは,項目1と項目3のエッジよりも大きいことを確認したい場合や項目1のノードのStrengthは項目2のノードのStrengthよりも大きいことを確認したい時です。これには,ブートストラップ差異検定(bootstrapped difference test)と呼ばれます。具体的には,比較したいエッジ(中心性指標)のブートストラップ値の差を計算して,その差の95%信頼区間を計算することで,0をまたぐかどうかで差の有無を判断できます。なお,この際に,0をまたぐことは,そこに差があることを示しますが,0をまたがないことでエッジや中心性指標が等しいとはいえない点に注意が必要です。
最もStrengthの高いgadbと最も低いgadfを比較します。bootnetパッケージのdifferenceTest関数で検討できます。実行すると,95%CIが0をまたいでいることが分かります。
differenceTest(accuracy_edge, 2, 6, "strength") ## # A tibble: 1 × 6
## id1 id2 measure lower upper significant
## <chr> <chr> <chr> <dbl> <dbl> <lgl>
## 1 gad7b gad7f strength -0.593 -0.408 TRUEエッジ間の差の検定結果をプロットします。それぞれのエッジ間で有意な差がある場合は黒く塗りつぶされ,有意ではない場合は灰色に塗りつぶされます。
plot(accuracy_edge, "edge", plot = "difference", onlyNonZero = TRUE, order = "sample") 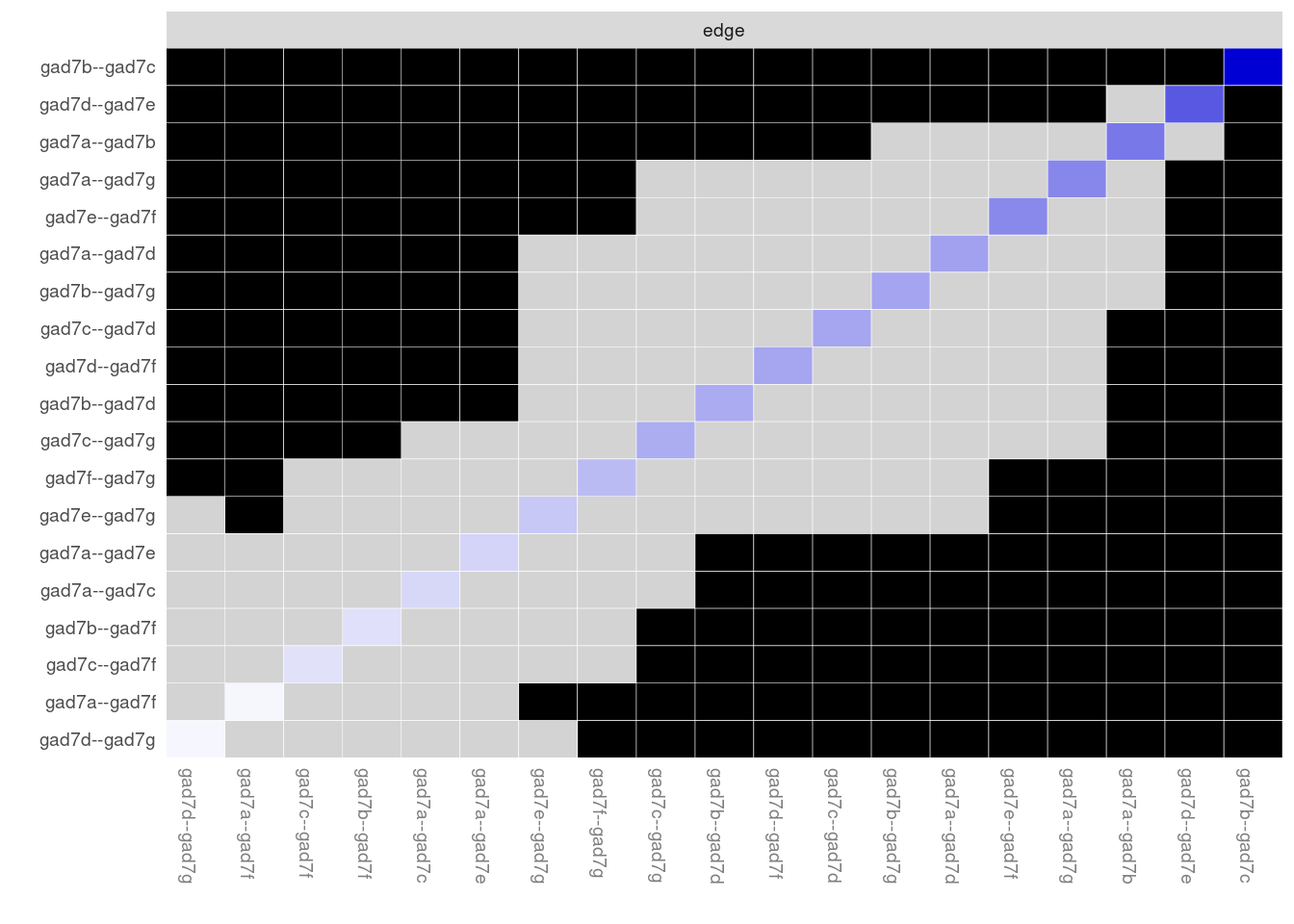
各ノード間のStrengthの差の検定結果をプロットします。それぞれのエッジ間で有意な差がある場合は黒く塗りつぶされ,有意ではない場合は灰色に塗りつぶされます。
plot(accuracy_edge,"strength")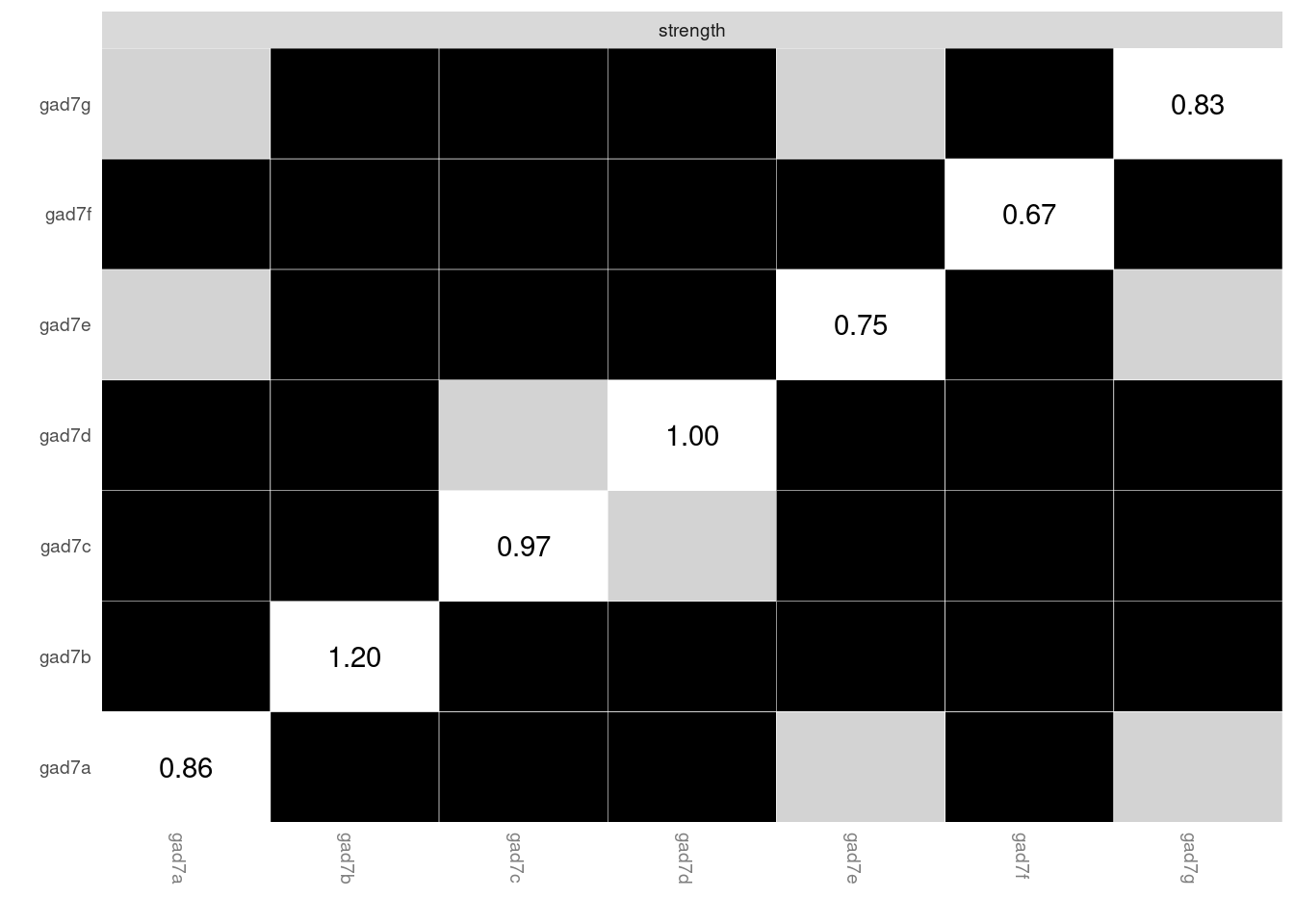
ブリッジ中心性
心理ネットワークの検討において,異なる症状項目のネットワークを示し,それぞれの症状ごとのまとまりをつなぐような項目を探すことがあります。例えば,うつ,社交不安,強迫症などの項目を含んだネットワークから,うつの特定の項目は,社交不安や強迫症にも影響が強いので,その項目がうつ,社交不安,強迫症の橋渡しをしているのではと検討する方法です。これを視覚的に検討することもできますが,ネットワークが大きなったり複雑化すると難しいため,ブリッジ中心性(Bridge centrality)という指標が提案されています(Jones, Ma, & McNally, 2021)。
ブリッジ中心性の指標
ブリッジ中心性では,各項目が所属するカテゴリーをネットワークのコミュニティ(community)と呼びます。つまり,うつ症状を測定する項目がいくつかあるとすれば,それらは「うつ症状」というコミュニティに所属します。その項目が所属するコミュニティと他のコミュニティとの関係を表すのがブリッジ中心性の指標になります。
bridge strength
bridge strengthは,あるノードから他のコミュニティへの接続の合計です。上記の例だと,うつ病症状の特定の項目から社交不安や強迫症のコミュニティに伸びているエッジの絶対値を合計したものです。bridge strengthで,その項目(ノード)が,所属外のコミュニティにどのくらいの影響力を持っているのかが分かります。
bridge closeness
bridge closenessは,あるノードから他のコミュニティの全てのノードまでの平均距離の逆数です。上記の例だと,うつ症状の特定の項目から社交不安や強迫症に所属する全ノードまでの距離(エッジの重みの逆数)を計算して平均化して,逆数を取ります。bridge closenessで,その項目(ノード)が,どのくらい他のコミュニティに近いのかが分かります。
bridge betweenness
bridge betweennessは,2つの異なるコミュニティからの任意の2つのノード間の最短経路上にそのノードがある回数です。上記の例だと,うつ症状の項目(ノード)が,うつ症状ノードと社交不安ノード間,うつ症状ノードと強迫症ノード間,社交不安ノードと強迫症ノード間の最短経路上に何度出てくるのかをカウントします。bridge betweennessで,その項目(ノード)が,コミュニティ間をどのくらい媒介しているのかが分かります。
Bridge expected influence
Bridge expected influenceは,あるノードの他のコミュニティへの接続の合計です。これだと,bridge strengthと同じに見えるのですが,エッジの絶対値をとって合計しないのがbridge strengthとの違いです。これによって正負に意味が出てきて,そのノードが他のコミュニティに全体的に負の影響を与えるのか正の影響を与えるのかが分かります。
Rでブリッジ中心性指標を計算する
さて,これまで使ってきたJordan et al.(2017)のデータを使ってブリッジ中心性指標を計算してみましょう。このデータでは,GAD-7(全般性不安)だけでなく,PHQ-9(うつ),PHQ-15(身体症状)も測定しています。以降では,3尺度のデータを使います。
data_bridge <- data %>%
rename(gad7a = S_GAD7_a, gad7b = S_GAD7_b, gad7c = S_GAD7_c, gad7d = S_GAD7_d,
gad7e = S_GAD7_e, gad7f = S_GAD7_f, gad7g = S_GAD7_g, phq9a = S_PHQ9_a,
phq9b = S_PHQ9_b, phq9c = S_PHQ9_c, phq9d = S_PHQ9_d, phq9e = S_PHQ9_e,
phq9f = S_PHQ9_f, phq9g = S_PHQ9_g, phq9h = S_PHQ9_h, phq9i = S_PHQ9_i,
phq15a = S_PHQ15_a, phq15b = S_PHQ15_b, phq15c = S_PHQ15_c, phq15d = S_PHQ15_d,
phq15e = S_PHQ15_e, phq15f = S_PHQ15_f, phq15g = S_PHQ15_g, phq15h = S_PHQ15_h,
phq15i = S_PHQ15_i, phq15j = S_PHQ15_j, phq15k = S_PHQ15_k, phq15l = S_PHQ15_l,
phq15m = S_PHQ15_m, phq15n = S_PHQ15_n, phq15o = S_PHQ15_o) %>%
select(gad7a, gad7b, gad7c, gad7d, gad7e, gad7f, gad7g,
phq9a, phq9b, phq9c, phq9d, phq9e, phq9f, phq9g, phq9h, phq9i,
phq15a, phq15b, phq15c, phq15d, phq15e, phq15f, phq15g, phq15h, phq15i,
phq15j, phq15k, phq15l, phq15m, phq15n, phq15o) 早速,3尺度の項目のネットワークを推定してみましょう。やり方は,上記と同じです。
res_bridge <- estimateNetwork(data_bridge,default = "EBICglasso", corMethod = "cor_auto")項目名があったが方が分かりやすいのでlabelをつけて,どのコミュニティに属しているのかをgroupで指定してプロットします。PHQ-9がPHQ15とGAD-7の間に挟まっている箇所がありますが,全体的に尺度ごとに分かれているように見えます。
label <- c("GAD7_1","GAD7_2","GAD7_3","GAD7_4","GAD7_5","GAD7_6","GAD7_7",
"PHQ9_1","PHQ9_2","PHQ9_3","PHQ9_4","PHQ9_5","PHQ9_6","PHQ9_7","PHQ9_8","PHQ9_9",
"PHQ15_1","PHQ15_2","PHQ15_3","PHQ15_4","PHQ15_5","PHQ15_6","PHQ15_7","PHQ15_8",
"PHQ15_9","PHQ15_10","PHQ15_11","PHQ15_12","PHQ15_13","PHQ15_14","PHQ15_15")
group <- list("GAD7"=c(1:7),"PHQ9"=c(8:16), "PHQ15"= c(17:31))
plot_res_bridge <- plot(res_bridge, layout = "spring", groups = group, labels = label)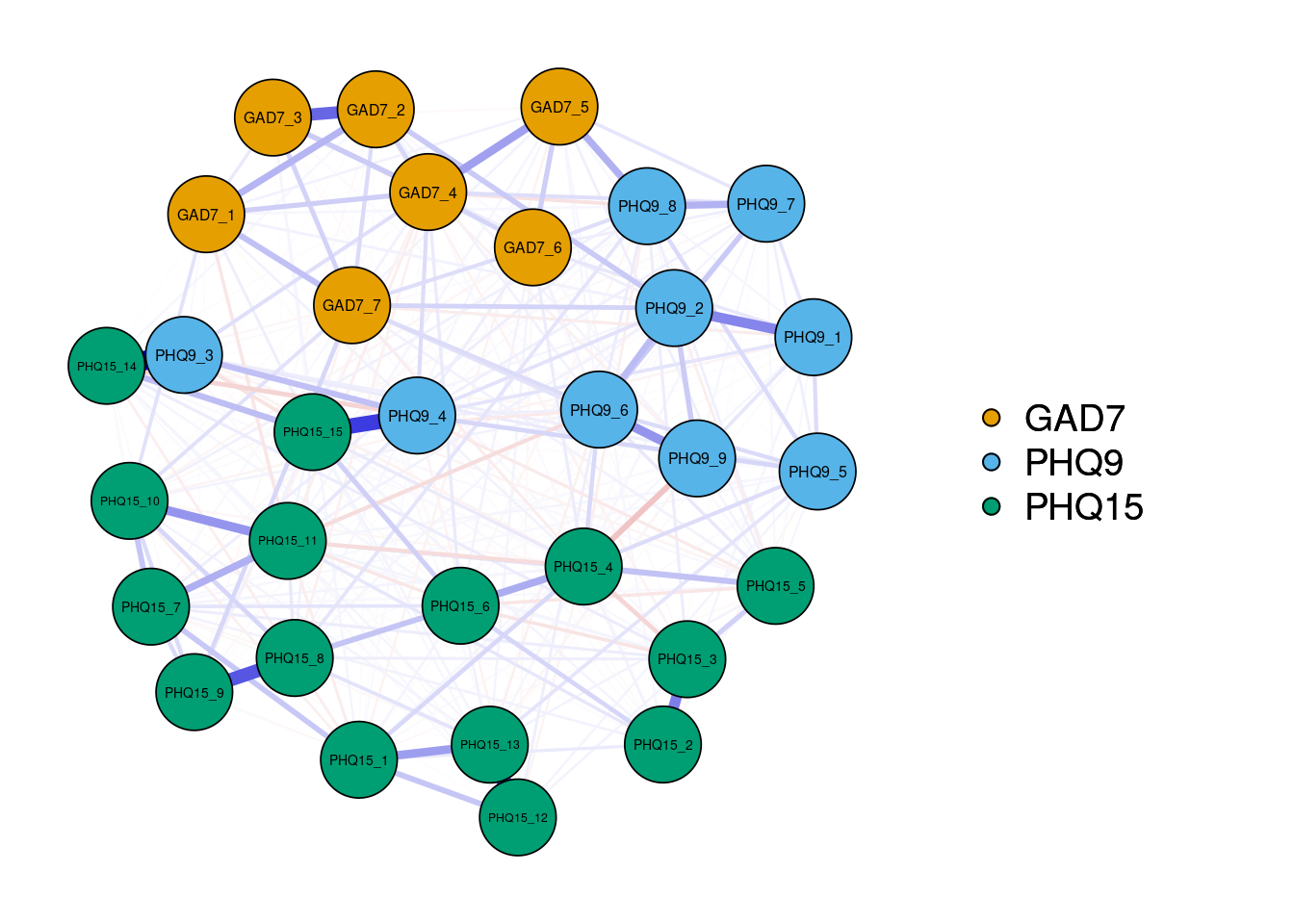
ブリッジ中心指標を計算してみましょう。networktoolsパッケージのbridge関数を使います。estimateNetwork()の出力を使うとうまく走りませんので,plotの内容をplot_res_bridgeに保存して,それを使っています。communitiesで各項目の所属を指定します(1がGAD-7, 2がPHQ-9, 3がPHQ-15です)。
library(networktools)
bridge_centrality <- bridge(plot_res_bridge,
communities=c('1','1','1','1','1','1','1',
'2','2','2','2','2','2','2','2','2',
'3','3','3','3','3','3','3','3','3','3','3','3','3','3','3'))ブリッジ中心性指標をプロットしてみましょう。なお,bridge関数では,Bridge Expected Influenceが1-stepと2-stepの2種類用意されています。両者の違いのは以下の通りです。
- Bridge Expected Influence (1-step): あるノードと異なるコミュニティにある他のノード間にあるエッジの値の合計です。
- Bridge Expected Influence (2-step): 1-Stepと同様だが,間接的な効果も考慮して計算している(つまり,ノードAからCに直接エッジがなくても,AからBを経由してCにいくエッジがあればカウントする。その際,はAからBのエッジの重みを用いる)。
Bridge Strength, Bridge Betweenness, Bridge Closenessを算出してみます。Bridge Strengthをみると,PHQ9の項目3(不眠)と4(気力低下)が高くなっており,これらのうつ項目が不安と身体症状によく接続していることが分かります。
plot(bridge_centrality, include = c("Bridge Strength",
"Bridge Betweenness",
"Bridge Closeness"))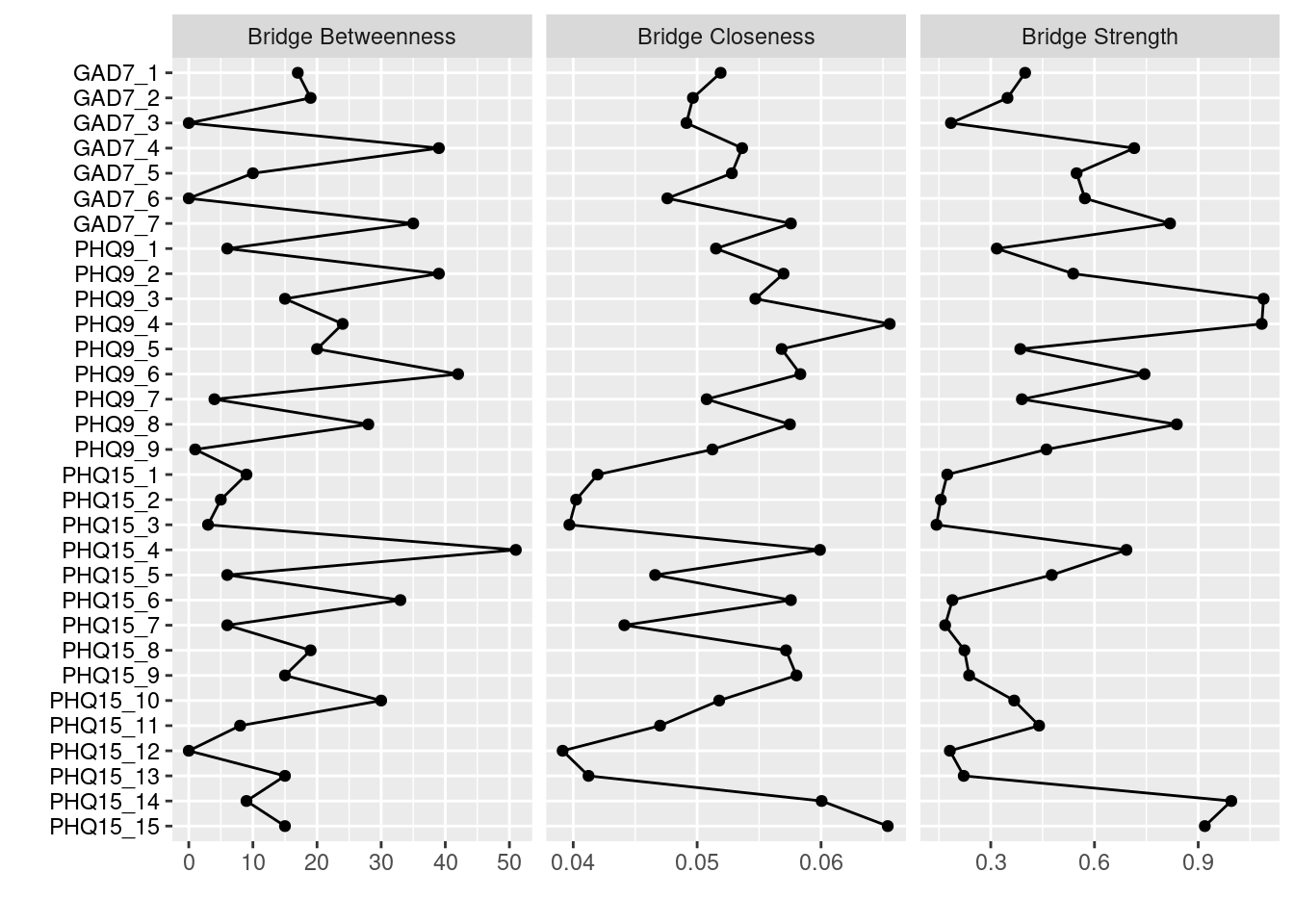
## Bridge Expected Influenceも計算する場合は以下を実行
#plot(bridge_centrality, include = c("Bridge Strength",
# "Bridge Betweenness",
# "Bridge Closeness",
# "Bridge Expected Influence (1-step)",
# "Bridge Expected Influence (2-step)"))bootnetでブリッジ中心性指標の安定性を検討できます。ただし,Bridge Expected Influencには対応していないようです。なお,国里のゼミ生でサーバーを使っている人は,コアは1つで実行してください。
stability_centrality_bridge <- bootnet(res_bridge, nBoots = 2500, type = "case", nCores =4, statistics = c("bridgeStrength","bridgeCloseness","bridgeBetweenness"), communities = group)CS係数を算出すると,このデータについては,bridgeClosenessのCS係数を係数が0.25以下ですので,解釈は避けたほうが良さそうです。
corStability(stability_centrality_bridge)## === Correlation Stability Analysis ===
##
## Sampling levels tested:
## nPerson Drop% n
## 1 851 75.0 216
## 2 1116 67.2 240
## 3 1381 59.4 222
## 4 1645 51.7 270
## 5 1910 43.9 244
## 6 2175 36.1 257
## 7 2440 28.3 245
## 8 2704 20.6 273
## 9 2969 12.8 268
## 10 3234 5.0 265
##
## Maximum drop proportions to retain correlation of 0.7 in at least 95% of the samples:
##
## bridgeBetweenness: 0.128
## - For more accuracy, run bootnet(..., caseMin = 0.05, caseMax = 0.206)
##
## bridgeCloseness: 0.517
## - For more accuracy, run bootnet(..., caseMin = 0.439, caseMax = 0.594)
##
## bridgeStrength: 0.75 (CS-coefficient is highest level tested)
## - For more accuracy, run bootnet(..., caseMin = 0.672, caseMax = 1)
##
## Accuracy can also be increased by increasing both 'nBoots' and 'caseN'.ブリッジ中心性指標の安定性をプロットします。
plot(stability_centrality_bridge, c("bridgeStrength","bridgeCloseness","bridgeBetweenness"))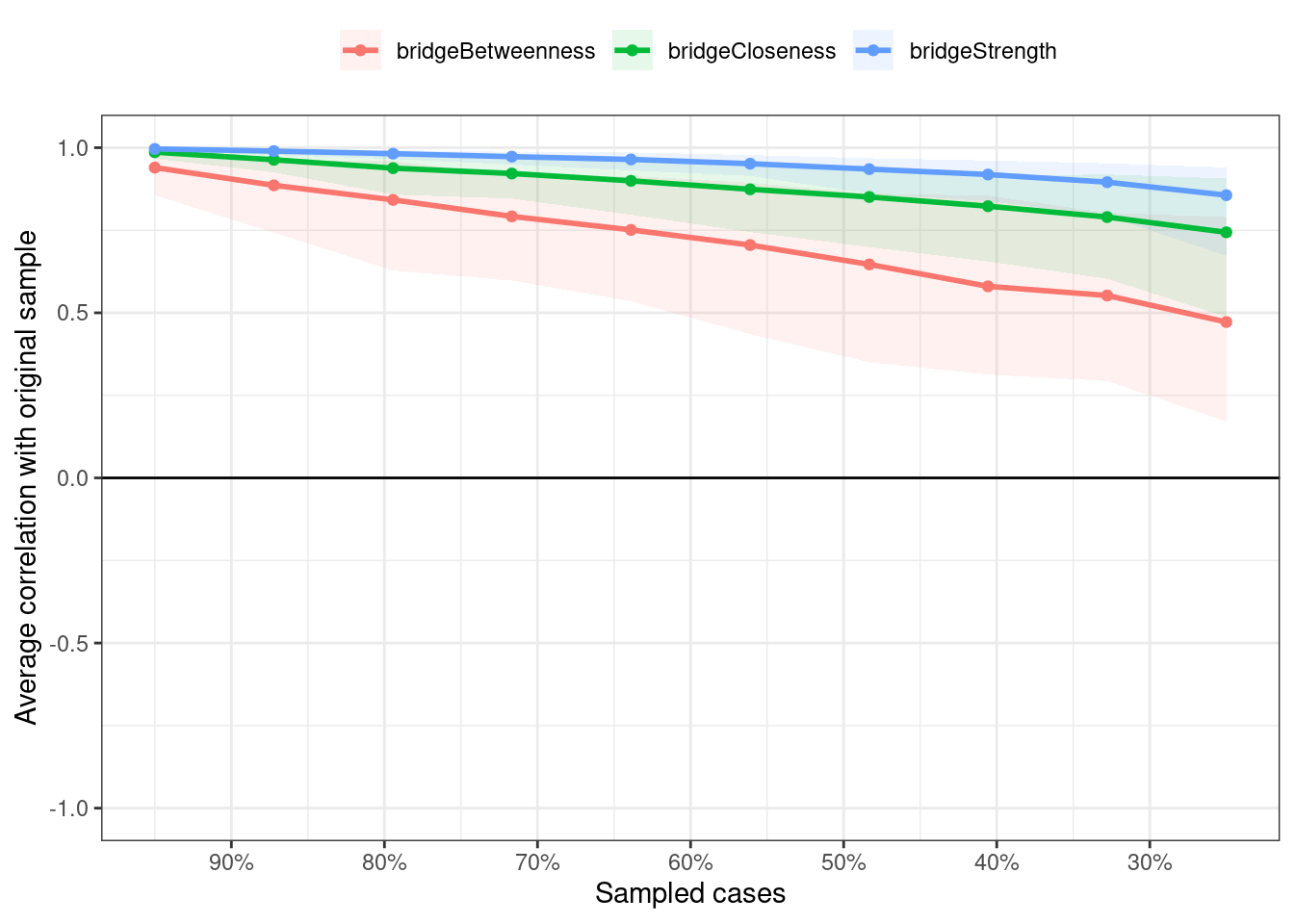
ネットワーク比較テスト
異なる集団間でネットワークを比較したいことがあるかもしれませんが,NetworkComparisonTestパッケージを使うとそれができます。以下では,男女でGAD-7のネットワークを比較してみます。まずは,データを整理して,男性のデータ(data_gad_male)と女性のデータ(data_gad_female)を用意します。
data_gad_gender <- data %>%
rename(gad7a = S_GAD7_a, gad7b = S_GAD7_b, gad7c = S_GAD7_c, gad7d = S_GAD7_d,
gad7e = S_GAD7_e, gad7f = S_GAD7_f, gad7g = S_GAD7_g) %>%
select(gad7a, gad7b, gad7c, gad7d, gad7e, gad7f, gad7g, gender) %>%
mutate(gender2 = if_else(gender == "Weiblich", 2, 1)) #1=male, 2= female
data_male <- data_gad_gender %>%
filter(gender2 == 1) %>%
select(-gender,-gender2) %>%
na.omit()
data_female <- data_gad_gender %>%
filter(gender2 == 2) %>%
select(-gender,-gender2) %>%
na.omit()男女別にネットワークを計算
集団ごとに分けたデータを用いて,estimateNetwork関数でネットワークを推定します。別々に推定をしており,そのままプロットすると比較がしにくいので,レイアウトが一致するように調整をします。プロットで集団間の違いを確認します。
network_male <- estimateNetwork(data_male, default = "EBICglasso", corMethod = "cor_auto")
network_female <- estimateNetwork(data_female, default = "EBICglasso", corMethod = "cor_auto")
L <- averageLayout(network_male, network_female)
Max <- max(abs(c(getWmat(network_male), getWmat(network_female))))
layout(t(1:2))
plot(network_male, layout = L, title = "Males", maximum = Max)
plot(network_female, layout = L, title = "Females", maximum = Max)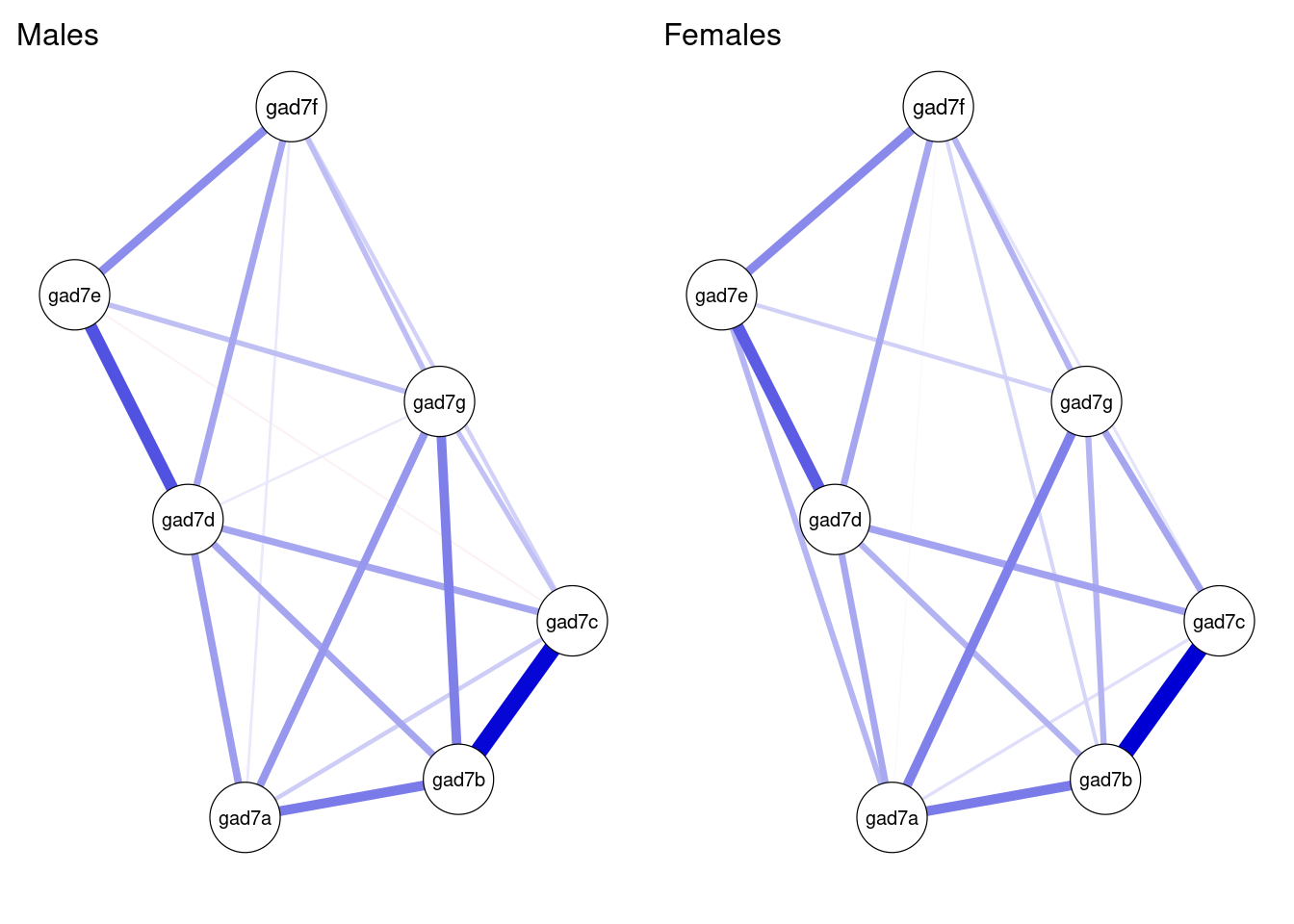
ネットワーク比較テスト
NetworkComparisonTestパッケージのNCT関数を使って, permutationベースの仮説検定を行います。NCTの引数では各データを引数にいれるのですが,NCTには”cor_auto”を使って自動で順序尺度を処理する機能はないので,bootnetで推定したネットワークをいれます(データでも推定したネットワークもどちらも可能です)。test.edgesとtest.centralityをTRUEにしてエッジと中心性指標を検定しましょう。
library(NetworkComparisonTest)
res_nct <- NCT(network_male, network_female, progressbar=FALSE, test.edges=TRUE, test.centrality=TRUE)結果をプロットしてみます。what=“network”で,ネットワーク構造の差異の検定結果が示されます。what=“strength” で,全体のStrengthの差異の検定結果が示されます。what=“edge”を指定すれば,個々のエッジの差異の検定結果が示されます。
plot(res_nct, what="network")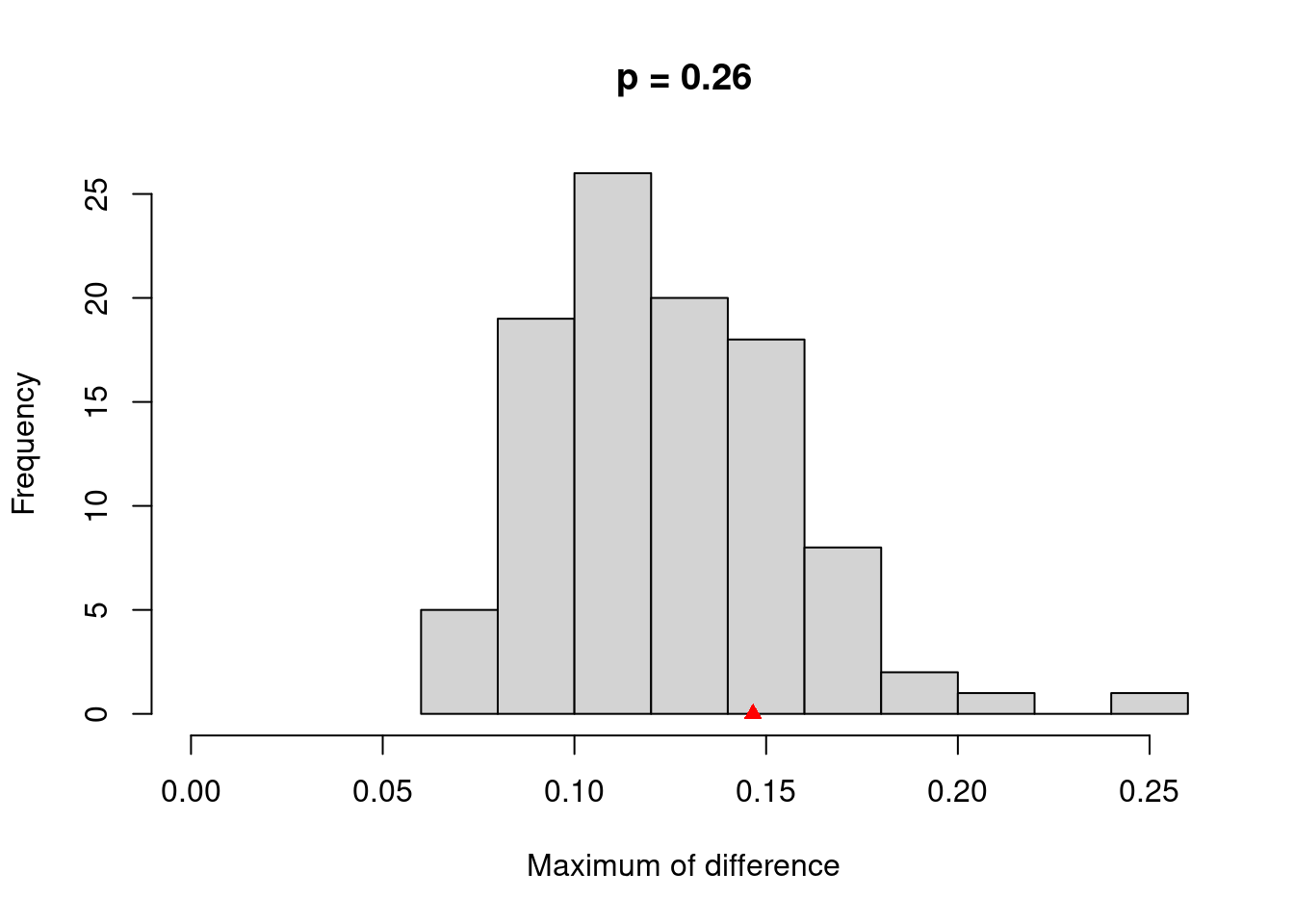
plot(res_nct, what="strength")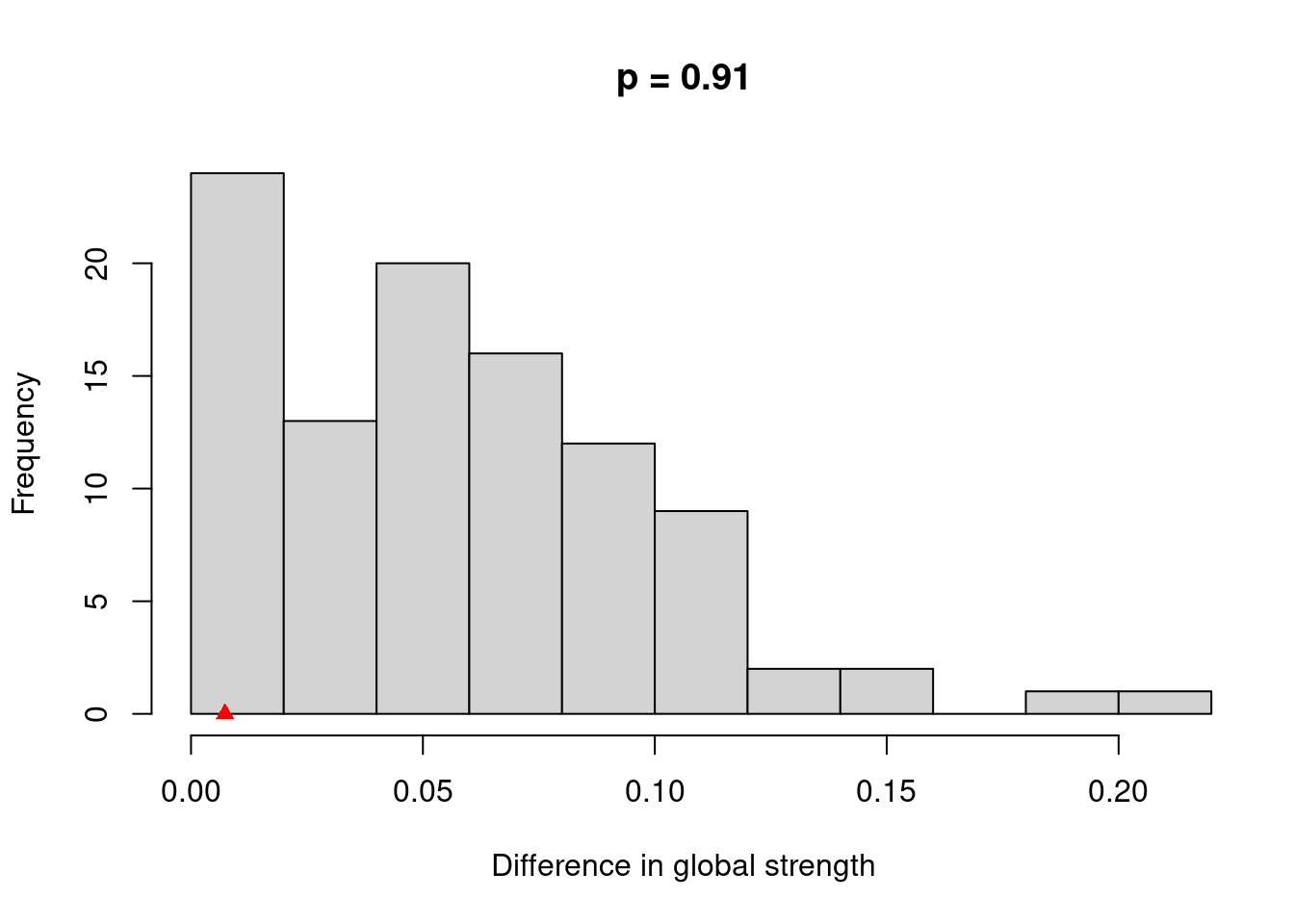
#plot(res_nct, what="edge")おわりに
心理ネットワークでの解析を概観してきましたが,心理ネットワーク分析手法は日進月歩です。どんどん新しい手法が提案されている現状がありますので,Psych Systemsのサイトを確認したり,そこで紹介されているサマースクールやワークショップに参加するのも良いかと思います。
文献
- Epskamp, S., Borsboom, D., & Fried, E. I. (2018). Estimating psychological networks and their accuracy: A tutorial paper. Behavior Research Methods, 50(1), 195–212.
- Epskamp, S., Waldorp, L. J., Mõttus, R., & Borsboom, D. (2018). The Gaussian Graphical Model in Cross-Sectional and Time-Series Data. Multivariate Behavioral Research, 53(4), 453–480.
- Epskamp, S., Borsboom, D., & Fried, E. I. (2018). Estimating psychological networks and their accuracy: A tutorial paper. Behavior Research Methods, 50(1), 195–212.
- Jones, P. J., Ma, R., & McNally, R. J. (2021). Bridge Centrality: A Network Approach to Understanding Comorbidity. Multivariate Behavioral Research, 56(2), 353–367.
- Jordan, P., Shedden-Mora, M. C., & Löwe, B. (2017). Psychometric analysis of the Generalized Anxiety Disorder scale (GAD-7) in primary care using modern item response theory. PloS One, 12(8), e0182162.